معمای ناتمام دکارت: ریاضیدانان مسئله هندسه ۳۸۰ ساله را حل کردند

به گزارش گروه دانشگاه خبرگزاری دانشجو، رنه دکارت ریاضیدان، دانشمند و فیلسوف فرانسوی بود که در ۳۱ مارس ۱۵۹۶ در لاهایه، تورین فرانسه متولد شد و در سن ۵۴ سالگی و در تاریخ ۱۱ فوریه ۱۶۵۰ در استکهلم، سوئد چشم از جهان فرو بست. رنه دکارت عموماً بنیانگذار فلسفه مدرن تلقی می‌شود، زیرا او یکی از اولین کسانی بود که از مکتب ارسطویی پیروی نکرد و اولین نسخه مدرن دوگانگی ذهن و بدن را که از آن مشکل ذهن و بدن ناشی می‌شود را تدوین کرد و بر این اساس علم جدیدی را که مبتنی بر مشاهده و آزمایش است، توسعه داد.

او با استفاده از یک سیستم شک علمی، دانش ظاهری ناشی از قدرت، حواس و عقل را کنار گذاشت و مبانی معرفتی جدیدی را بر اساس این شهود که وقتی تفکر است، وجود جریان دارد را بنا کرد. رنه دکارت این تئوری خود را در قالب جمله مشهور من فکر می‌کنم، بنابراین من هستم بیان کرد. این تئوری در زبان لاتین به صورت Cogito، ergo sum شناخته شده است. اگر چه این تئوری در اصل به زبان فرانسه نوشته شده و عبارت از «ژو پنسه، دونک ژو سوئی» (Je pense، donc je suis) است. دکارت یک دوگانگی متافیزیکی ایجاد کرد که بین ذهن که جوهر آن تفکر است و ماده که جوهر آن امتداد در سه بعد است تمایز قائل می‌شود. متافیزیک دکارت بر اساس فلسفه عقلانی و بر پایه بدیهی شمردن ذهن، ماده و خدا است، اما فیزیک و فیزیولوژی او بر اساس تجربه حسی، مکانیکی و تجربی است.

آن زمان را می‌توان نوعی انقلاب علمی قلمداد کرد که نه تنها حجیت علم قرون وسطی بلکه حتی اعتبار جهان باستانی را برانداخت. زیرا نه تنها به خسوف فلسفه مدرسی انجامید، بلکه به دوران تسلط طبیعیات ارسطویی هم پایان می‌داد. با این وجود بسیار مهم است که در نظر بگیریم دکارت و بسیاری از پیروانش (به جز پاسکال) با خوشبینی وافر به عقل، اعتقاد داشتند که تلاش فکری‌شان به خداشناسی‌ای منجر می‌شود که در آن انسان دیگر نه با اتکا به متنی مقدس یا اعتماد به برخی عالمان یا دینداران (اصحاب کلیسا) بلکه صرفا با تکیه بر عقل و دانش خود می‌تواند وجود خداوند، وجود روح و تمایز آن از بدن، ملکوت خداوند، خلقت جهان از عدم، لزوم اعتقاد به خداوند، پیروی از فرامین او و ده‌ها موضوع دیگر را دریابد و به تشویش‌های مذهبی پایان دهند.

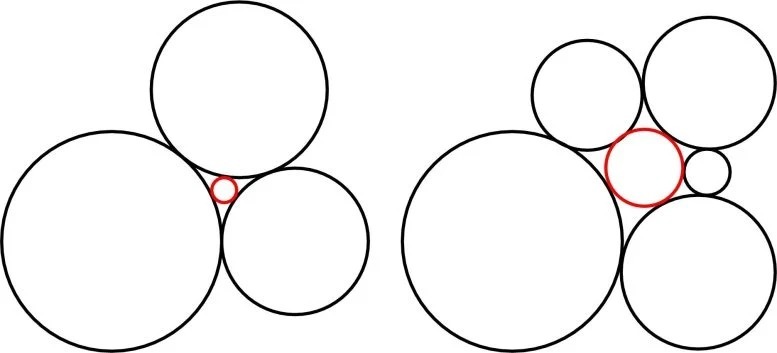
در هندسه اقلیدسی قضیه دکارت بیان می‌کند که به ازای هر چهار دایرهٔ در حال «بوسه»، یا دایره‌هایی که به‌صورت مشترک مماسند، شعاع‌های دایره‌ها در یک معادله درجه دو صدق می‌کنند. با حل کردن این معادله می‌توان یکی از این دایره‌ها را با داشتن سه دایرهٔ دیگر ترسیم کرد. این قضیه نامش را از رنه دکارت گرفته است که آن را در سال ۱۶۴۳ در نامه‌ای به لیزابت پالاتینی، دختر فردریک پنجم و الیزابت استوارت بیان کرده بود.

امروز پس از گذشت چند قرن از آن دوران، ریاضیدانان دانشگاه موناش پازلی را شکستند که قدمت آن به قرن هفدهم بازمی‌گردد و قضیه دایره دکارت را به یک قلمرو جسورانه جدید گسترش داده است.

این تیم با استفاده از ابزار‌های ریاضی پیشرفته الهام گرفته از فیزیک، یک معادله کلی برای هر تعداد دایره مماس به دست آورده است که بینش جدیدی را در رابطه با معادله‌ای که در اصل توسط ریاضیدان رنه دکارت پیشنهاد شده بود، ارائه می‌دهد.

قضیه دکارت، سنگ بنای هندسه، رابطه بین چهار دایره مماس متقابل را تعریف می‌کند. اما برای قرن‌ها، تعمیم معادله به بیش از چهار دایره، ریاضیدانان را از خود دور کرده بود.

دانشیار دانیل ماتیوس از دانشکده ریاضیات دانشگاه موناش، همراه با کاندیدای دکترا اوریون زیماریس، معادله‌ای را که بر "n-گل ها" حاکم است، یعنی الگو‌های هندسی پیچیده‌ای که توسط پیکربندی‌های بزرگتر از دایره‌های مماس تشکیل می‌شوند، شناسایی کرده‌اند.

در تئوری بسته بندی دایره‌ای، گل‌ها به عنوان یک بلوک ساختمانی اساسی عمل می‌کنند.

به خوبی ثابت شده است که وقتی انحنای دایره‌های بیرونی (گلبرگ ها) در یک گل n مشخص شد، انحنای دایره مرکزی را می‌توان دقیقاً تعیین کرد.

محققان مطالعه خود را بر اساس تکنیک‌های ریاضی مدرن شامل اسپینور‌ها - موجودات ریاضی که در مکانیک کوانتومی و نسبیت نیز ظاهر می‌شوند - استوار کردند.

از دکارت تا اسپینور

دکارت در سال ۱۶۴۳ برای پرنسس الیزابت پالاتینات مشکلی را مطرح کرد، با این فرض که او می‌تواند آن را حل کند. بالاخره او مختصات دکارتی را اختراع کرده بود! اما نتوانست، و زمانی که مسئله را به یک مسئله عملاً قابل حل تغییر داد، این به عنوان قضیه کلاسیک انتشار دایره دکارت شناخته شد.

این معادله برای اولین بار توسط یاماجی نوشیزومی در سال ۱۷۵۱ پیشنهاد شد و چندین بار به طور مستقل دوباره کشف شد - توسط یاکوب اشتاینر در سال ۱۸۲۶، ویلیام بیکرافت در سال ۱۸۴۲ و فردریک سودی در سال ۱۹۳۶، که به طرز معروفی آن را در قالب یک شعر بازنویسی کرد.

دیگران نتیجه را به روش‌های دیگری تعمیم داده‌اند، اما این اولین بسط نتیجه است که یک معادله صریح را به دست می‌دهد که شعاع‌های تعداد دلخواه دایره را در صفحه مربوط می‌کند.

زیماریس، که تحقیقات دکترای او منجر به موفقیت شد، ارتباطات غیرمنتظره با سایر زمینه‌های ریاضی و فیزیک را برجسته کرد وذ گفت: رویکرد ما از ابزار‌های هندسی پیشرفته با الهام از فیزیک استفاده کرد که شگفت‌انگیز بود.

او با بیان اینکه اسپینور‌ها که معمولاً در مکانیک کوانتومی استفاده می‌شوند، نقش کلیدی در رویکرد آنها داشتند، افزود: ما از نسخه‌ای از اسپینور‌ها استفاده کردیم که توسط راجر پنروز برنده جایزه نوبل و ولفگانگ ریندلر ساخته شده بود و آنها آن را در نظریه نسبیت به کار بردند.

به نظر می‌رسد که همان ساختار‌های ریاضی که اسپین کوانتومی و نسبیت را توصیف می‌کنند نیز به ما در درک بسته بندی دایره کمک می‌کنند.

یک پیروزی برای ریاضیات محض و یک تیم در حال رشد

این کار نه تنها یک گام مهم به جلو در ریاضیات محض را نشان می‌دهد، بلکه قدرت رو به رشد گروه توپولوژی در دانشگاه موناش را نیز به نمایش می‌گذارد، که اکنون شامل ۹ دانشجوی دکترا است که پنج نفر از آنها زن هستند.

ماتیوس گفت: این کشف نمونه‌ای هیجان انگیز از این است که چگونه مسائل کلاسیک می‌توانند الهام بخش ریاضیات جدید قرن‌ها بعد باشند.

باورنکردنی است که فکر کنیم سوالی که دکارت در دهه ۱۶۰۰ با آن دست و پنجه نرم می‌کرد هنوز پاسخ‌های جدیدی در انتظار یافتن دارد.

این تحقیقات موفقیت آمیز در مجله هندسه و فیزیک منتشر شده است.

مرجع: "قضیه دایره اسپینورها و دکارت" توسط دانیل وی. ماتیوس و اوریون زیماریس، 25 فوریه 2025، مجله هندسه و فیزیک .
DOI: 10.1016/j.geomphys.2025.105458